Interval (musik)
Interval (fra lat. intervallum - gap, afstand; forskel, ulighed) i musik - forholdet mellem to musikalske lyde efter deres højde [1] . I europæisk musikteori har hele tonen været et mål for beregning af musikalske intervaller i århundreder , i forhold til hvilke både mindre (for eksempel halvtone , kvarttoner) og nogle større (for eksempel diton , halvtoner , tritoner ) intervaller blev bestemt. Det mindste musikalske interval i den europæiske tradition anses for at være en halvtone . Intervaller mindre end en halvtone kaldes mikrointervaller.. Konsonant- og dissonantintervaller er de vigtigste elementer i harmoni .
To sider af intervallet
På den ene side kan intervallet repræsenteres som en matematisk ( akustisk ) værdi, der udtrykker forholdet mellem to tal - frekvenserne af de vigtigste harmoniske af de lyde, der er inkluderet i det . I de teoretisk "korrekte", det vil sige de mest naturligt klingende intervaller, bør frekvenserne relateres som små heltal, for eksempel 3:2 for en kvint [2] [3] . I lige temperament afviger forholdene lidt fra "korrekt" (f.eks. 1,498307 i stedet for 3:2). Nogle gange bruges i stedet for forholdet den ækvivalente værdi af forskellen i logaritmerne af frekvenserne ( cent for 3:2). Den absolutte matematiske værdi af intervallet er fastsat ved mekaniske (på en monochord osv.) eller elektroniske (ved hjælp af et anvendt computerprogram) målinger.
På den anden side er intervallet en kategori af specifikt musikalsk logik, som allerede manifesterer sig i musikalsk terminologi. For eksempel antyder udtrykket quinta konceptet med fem trin af den diatoniske skala (det femte trin [quinta vox] beregnes ud fra bunden af intervallet, som kaldes "prima"). Ud fra den kontekst, som nodeskrivning giver (bogstav, lineær osv.), er det den musikalsk-logiske værdi af intervallet, der udledes.
Et interval som en matematisk (akustisk) størrelse kan ikke entydigt forbindes med et noteret musikalsk interval. For eksempel fortolkes notationen eis-a ("mi skarp" - "la") i den klassiske harmonidoktrin som et kromatisk interval (reduceret kvart , hvilket betyder opløsningen af mi skarp i f skarp), enharmonisk lig med dur tredjedel af et ensartet temperament , kan det i en anden sammenhæng betyde både den pythagoræiske diton og den store tredjedel af den rene skala (f.eks. i den italienske madrigal i det 16. århundrede). Intervallet, noteret som fis-a ("F skarp" - "la"), i tonearten C-dur (C-dur) kan betragtes som en lille tredjedel af et jævnt hærdet system og i tetrachordet af kromatisk slægt blandt grækerne - som en halv-toraton eller halv- diton osv.
Da notationen kun fikserer den musikalske (og ikke den matematiske) side af intervallerne, giver spørgsmålet om den akustiske "ægthed" af lyden af denne eller hin musik ( især tidlig musik ) ikke mening. Tvetydigheden i forholdet mellem intervallets "nummer" og " harmoniske logik" åbner mulighed for musikologiske og udførende fortolkninger af noteret musik.
Klassifikation af intervaller
Den nederste lyd af intervallet kaldes basen, den øverste lyd kaldes toppen. Intervaller er klassificeret:
1. Ved at tage: simultan (harmonisk eller "lodret", interval) eller sekventiel (melodisk eller "horisontal", interval) [4] .
2. Ved volumen (antal) af trin, der er indesluttet i dem . Tallet, der angiver antallet af trin i et interval, er også en forkortelse for det interval. Intervaller fra prima til en oktav kaldes simple , over en oktavsammensætning . Sammensatte intervaller arver egenskaberne af simple (for eksempel kan ingen, ligesom sekunder, være store og små) [5] . Intervaller bredere end en dobbeltoktav (kvintdecim) er traditionelt ikke betragtet i elementær musikteori.
3. Ved "kvalitet". Et intervals "kvalitet" bestemmes af ordene "stor" (forkortet b. ), "lille" ( m. ), "ren" ( h. ), "forøget" ( uv. ), "reduceret" ( min. . ), "to gange forøget"( dv. uv. ) og "to gange reduceret" ( dv. um. ), hvilket tydeliggør intervallets kvantitative karakteristika.
- Udtrykkene "stor" og "lille" refererer til intervallerne på sekunder, tredjedele, sjettedele og syvende.
- Udtrykket "ren" refererer til intervallerne prima, quarts, kvinter og oktaver.
4. Ifølge graden af eufoni. Fra antikken til æraen med dur-mol tonalitet blev intervaller også fordelt efter, hvor sømløst de opfattes af øret (for flere detaljer, se artiklen Konsonans og dissonans ). I forskellige historiske klassifikationer udpegede teoretikere (i rækkefølge fra de mest vellydende til de mest dissonante) "perfekte konsonanser", "uperfekte konsonanser", "uperfekte dissonanser", "perfekte dissonanser" og andre evaluerende udtryk.
Forøgede og reducerede intervaller
I elementær dur-mol musikteori indebærer udtrykkene "nedsat" og "øgede" intervaller en ændring i antallet af toner i et interval, mens antallet af trin forbliver uændret [6] .
- Øget - hovedtypen af interval (ren eller stor) øges med en halvtone.
- Reduceret - hovedtypen af interval (ren eller lille) sænkes med en halvtone (undtagen "prima").
- Dobbelt forstærket - hovedtypen af interval (ren eller stor) øges med en hel tone.
- To gange formindsket - hovedtypen af interval (ren eller lille) reduceres med en hel tone (bortset fra "prima" og "mindre sekund").
Eksempler:
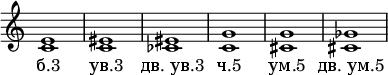
I musik, hvor der ikke er nogen dur-mol tonalitet (for eksempel i dodekafonien af komponister fra New Vienna School), mister begreberne "reduceret" og "øget" deres betydning, og udtrykket "ren" bruges kun i følelse af akustisk renhed (se Pure tuning ).
Liste over musikalske intervaller
De følgende tabeller illustrerer typerne af intervaller, som de er standard beskrevet i manualer om elementær musikteori fra det 20. århundrede (f.eks. i ETM af B. Alekseev og A. Myasoedov [7] ).
| Antal trin |
Navn | Slags | Antal toner |
Betegnelse |
|---|---|---|---|---|
| Simple intervaller | ||||
Eksempler på simple harmoniske intervaller:
| ||||
| en | Prima | ren | 0 ( unisont ) | del 1 |
| 2 | Sekund | lille stor |
0,5 ( halvtone ) 1 ( heltone ) |
m.2 b.2 |
| 3 | Tredje | lille stor |
1,5 ( halv-diton ) 2 ( diton ) |
m.3 b.3 |
| fire | Quart | nettet forstørret |
2,5 3 ( triton ) |
del 4 uv.4 |
| 5 | Quint | reduceret netto |
3 (triton) 3,5 |
sind.5 h.5 |
| 6 | Sjette | lille stor |
4 4,5 |
m.6 b.6 |
| 7 | Syvende | lille stor |
5 5,5 |
m.7 b.7 |
| otte | Oktav | ren | 6 | del 8 |
| Sammensatte intervaller | ||||
Eksempler på sammensatte harmoniske intervaller:
| ||||
| 9 | Nona (sekund + h.8) | lille stor |
6,5 7 |
m.9 b.9 |
| ti | Decima (tredje + del 8) | lille stor |
7,5 8 |
m.10 b.10 |
| elleve | Undecima (quart + del 8) | nettet forstørret |
8,5 9 |
del 11 uv.11 |
| 12 | Duodecima (femte + del 8) | reduceret netto |
9 9,5 |
sind.12 h.12 |
| 13 | Tertsdecima (sexta + del 8) | lille stor |
10 10,5 |
m.13 b.13 |
| fjorten | Quartdecima (septima + del 8) | lille stor |
11 11,5 |
m.14 b.14 |
| femten | Quintdecima (oktav + h.8) | ren | 12 | del 15 |
| Antal trin | Navn | Kvalitet | Antal toner | Betegnelse | Quint trin |
| en | Prima | ren | 0 | del 1 | 0 |
| forstørret | 0,5 | SW.1 | 7 | ||
| 2 | Sekund | lille | 0,5 | m.2 | 5 |
| stor | en | b.2 | 2 | ||
| forstørret | 1.5 | SW.2 | 9 | ||
| reduceret | 0 | sind.2 | 12 | ||
| 3 | Tredje | lille | 1.5 | m.3 | 3 |
| stor | 2 | b.3 | fire | ||
| reduceret | en | sind.3 | ti | ||
| forstørret | 2.5 | SW.3 | elleve | ||
| fire | Quart | ren | 2.5 | del 4 | en |
| forstørret | 3 | SW.4 | 6 | ||
| reduceret | 2 | sind.4 | otte | ||
| 5 | Quint | ren | 3.5 | del 5 | en |
| reduceret | 3 | sind.5 | 6 | ||
| forstørret | fire | SW.5 | otte | ||
| 6 | Sjette | lille | fire | m.6 | fire |
| stor | 4.5 | b.6 | 3 | ||
| reduceret | 3.5 | sind.6 | elleve | ||
| forstørret | 5 | SW.6 | ti | ||
| 7 | Syvende | lille | 5 | m.7 | 2 |
| stor | 5.5 | b.7 | 5 | ||
| forstørret | 6 | SW.7 | 12 | ||
| reduceret | 4.5 | sind.7 | 9 | ||
| otte | Oktav | ren | 6 | del 8 | 0 |
| reduceret | 5.5 | sind.8 | 7 |
I det tolvtrins lige temperamentsystem , som er blevet det vigtigste i europæisk musik siden det 18. århundrede, beregnes forholdet mellem frekvenserne af de lyde, der danner intervallet , hvor er antallet af toner (se tabellen ovenfor) .
Appeller
Inversionen af et interval er bevægelsen af lyden, der ligger ved dens base, en oktav op eller toppen af intervallet - en oktav ned. Når det vendes om, vendes kvaliteten af intervallet: et stort bliver lille, et forstørret interval bliver reduceret, et dobbeltforøget interval bliver to gange formindsket og omvendt. Et rengøringsinterval forbliver rent. I simple intervaller er summen af de digitale betegnelser for hovedtypen af interval og dets inversion altid lig med ni.
| Grundlæggende afstand | Inverteret interval |
|---|---|
| Prima (1) | Oktav (8) |
| Anden (2) | Septima (7) |
| Tredje (3) | Sexta (6) |
| Quart (4) | Quinta (5) |
| Quinta (5) | Quart (4) |
| Sexta (6) | Tredje (3) |
| Septima (7) | Anden (2) |
| Oktav (8) | Prima (1) |
Hvis det er nødvendigt at vende et sammensat interval, overføres begge dets lyde til en oktav (øvre - nede, nedre - op) eller en af dem til to oktaver, mens summen af de digitale betegnelser for begge intervaller altid er lig med seksten.
| Grundlæggende afstand | Inverteret interval |
|---|---|
| Nona (9) | Septima (7) |
| Decima (10) | Sexta (6) |
| Undecima (11) | Quinta (5) |
| Duodecyma (12) | Quart (4) |
| Terzdecima (13) | Tredje (3) |
| Quartdecima (14) | Anden (2) |
| Quintdecima (15) | Prima (1) |
En øget oktav, også betragtet som et sammensat interval, giver en nedsat oktav i omløb.
Noter
- ↑ Nazaikinsky E. V. Interval Arkivkopi dateret 16. april 2018 på Wayback Machine // Great Russian Encyclopedia. Bind 11. - M., 2008. - S. 435.
- ↑ I hjemlig musikvidenskab kaldes det numeriske forhold mellem intervallet ofte forkert " proportion ". For eksempel, E.V. Gertsman: "... klingende skal udtrykkes med et tal... man kan sikkert repræsentere sunde relationer med specifikke numeriske proportioner. Men da ulige mængdeforhold er repræsenteret af forskellige typer proportioner, kan afstandene mellem lyde (intervaller) registreres på en lignende måde, det vil sige multiple, epimorale, epimeriske og andre proportioner ”(Pythagorean musicology. SPb., 2003, s. 280-281. ).
- ↑ Detaljer om de aritmetiske termer "forhold" og "proportion" kan findes i aritmetiske lærebøger, for eksempel i sjette afsnit af A. S. Kiselevs lærebog "Systematic Arithmetic Course" Arkiveksemplar dateret 4. december 2016 på Wayback Machine .
- ↑ Udtrykkene "horisontalt interval" og "lodret interval" kom i brug i de sidste årtier af det 20. århundrede, se for eksempel: Kholopov Yu. N. Harmony. Teoretisk kursus. M., 1988, s.22. I de hidtil populære lærebøger i elementær musikteori, skrevet i 1950'erne. - I. V. Sposobina (1951), V. A. Vakhromeev (1956) såvel som i "Praktisk guide til musikalsk literacy" af G. A. Fridkin (1957) - kun udtrykkene (henholdsvis) "melodisk interval" og "harmonisk interval.
- ↑ Interval // Kasakhstan. National Encyclopedia . - Almaty: Kasakhiske encyklopædier , 2005. - T. II. — ISBN 9965-9746-3-2 . (CC BY SA 3.0)
- ↑ Alekseev, Myasoedov, 1986 , s. 69.
- ↑ Alekseev, Myasoedov, 1986 , s. 67, 70.
- ↑ Bityukov Sergey. 13 lyde og intervaller. Deres opfattelse og betegnelse. Frets af afvigelse og modulering (russisk) ? . Habr (7. august 2021). Hentet 12. august 2021. Arkiveret fra originalen 12. august 2021.
Litteratur
- Alekseev B., Myasoedov A. Intervals // Elementær Musikteori. - M . : Musik, 1986. - S. 64-78. - 240 sek.
- Interval // Musical Encyclopedia. - M . : Soviet Encyclopedia, 1974. - T. 2. - S. 544-545. — 960 s.
- Solovyov N.F. Interval // Encyclopedic Dictionary of Brockhaus and Efron : i 86 bind (82 bind og 4 yderligere). - Sankt Petersborg. , 1890-1907.
- Fridkin G. En praktisk guide til musikalsk læsefærdighed. — M.: Muzgiz, 1962
Links
- Hugo Riemanns intervaltabeller
- Tabel 365 over intervaller (navne på intervaller og deres oversættelser er ikke normative)
| |
|
|---|---|
| I bibliografiske kataloger |
|
| Musikalske intervaller | ||
|---|---|---|
| Enkel | ||
| Sammensatte | ||
| Mikrointervaller | ||
| Særlig | ||




